Go]
				[Back
				[Home

[Il tempo e l'entropia]

Tutto parte sempre dall' avere un problema e quindi cercare di risolverlo. Il percorso che porta alla genesi della funzione entropia, passa sinteticamente attraverso due problemi:

L' estensione del Teorema di Conservazione dell' energia ai processi dissipativi.

La razionalizzazione dell' Impossibilit� del Moto Perpetuo di II specie.

Se non conoscete il Teorema di Conservazione dell' Energia, in breve si pu� enunciare come l' energia meccanica di un sistema � costante, (ricordando che quest' ultima � data dalla somma di energia cinetica ed energia potenziale). Questo � uno dei cardini della fisica, � un mezzo di indagine potentissimo, non tanto quanto l'equazione della forza Newtoniana ( F=ma), ma � un suo valido sostituto per lo studio del moto dei punti materiali. Alle spalle di questo semplice teorema c'� un formalismo matematico molto pesante, che non permette ai non-addetti ai lavori di poterlo affrontare. Comunque noi vogliamo capire pi� che la formulazione matematica, il senso fisico del teorema, quindi non preoccupiamoci pi� di tanto, e continuiamo con la nostra ricerca. Questo teorema, forse non tutti sanno che � valido solo in un campo cosiddetto conservativo. Questo significa che il lavoro necessario per portare un oggetto , ad esempio da A a B , � indipendente dal cammino, cio�, voi per portare una massa M in cima ad una montagna se la spingete su lungo il pendio oppure se la issate con una carrucola lungo lo strapiombo, compite lo stesso lavoro. Questo voi mi direte che � ovviamente falso ed infatti tutte le vostre esperienze non possono aver mai constatato la veridicit� di questa affermazione. Ma esiste una spiegazione molto semplice a questo fatto, nessuno di noi ha mai esperito la vita in assenza totale di attriti. Sono proprio loro che ci fanno fare pi� fatica per vivere, e ovviamente essendo una condizione puramente ideale, e forse impossibile da realizzare , rendono pressoch� inutile il teorema di conservazione dell' energia, che vale solo sotto questa ipotesi. Ma allora come fanno i fisici ad andare avanti !! Behh � semplice perch� come dice il proverbio: "Fatta la legge , fatto l'inganno." E i nostri bravi fisici sono riusciti a trovare una formuletta che desse loro la possibilit� di estendere il teorema di conservazione dell' energia anche in presenza di forze dissipative.
Ed ecco qua che salta fuori il Primo Principio della Termodinamica, ossia

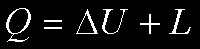
Ora che sappiamo cosa sia il I principio possiamo fare degli esperimenti per vedere se vale, ossia se � una buona definizione. Ma ecco che a questo punto scopriamo che se cerchiamo di trasformare il lavoro in calore e poi il calore di nuovo in lavoro, non otteniamo la quantit� di partenza. Quindi qualcosa viene perso nel processo, se ne deduce che non � lecito scrivere che in un ciclo "la quantit� di calore � uguale al lavoro", srcitta in formula dQ=dL . Grazie al lavoro di Carnot, Joule, Kelvin ed altri siamo riusciti a trovare una formulazione fisica di questa perdita di energia. Ovviamente, per� prima della formula arriva la parola e quindi ecco che troviamo due enunciati a parole di quello che � stato chiamato il II principio della Termodinamica. Questi enunciati sono da attribuirsi il primo a Clausius e il secondo a Kelvin, e citano cos�:

E’ impossibile ottenere una trasformazione il cui unico risultato sia quello di :

trasferire calore da un corpo pi� freddo ad uno pi� caldo.

estrarre calore da una sorgente e convertirlo in lavoro.

Questi due enunciati del II principio ci danno delle utili informazioni su quello che non � consentito fare, mentre quello che � consetito non � esplicitamente espresso. Vediamo allora di cosa si tratta. Per poter investigare al meglio questo campo � utile, se non addirittura indispensabile, guardare come variano le quantit� in un ciclo, poich� in un ciclo abbiamo che DU = 0 , cio� l’ energia interna ad un sistema non varia , questa condizione ci permette di uguagliare Q ad L che non solo sono le quantit� che ci interessano ma, cosa ancora pi� importante, la relazione che li unisce � proprio quello di uguaglianza che � quella che abbiamo visto darci dei problemi, per la sua non sempre veridicit�. Ebbene si pu� dimostrare che una macchina termica che lavori in un ciclo ideale, cio� costituito solo da processi reversibili , ha come rendimento 1 , e questo rendimento rappresenta un limite oltre al quale non si pu� andare. Notiamo per� che a differenza del moto perpetuo di I specie, dovuto alla presenza degli attriti, che ha un limite soltanto tecnologico ossia pi� la tecnologia migliora pi� in l� viene spostato il limite, il concetto rendimento limite non � subordinato alla tecnologia, esso esiste ed � quello per sempre, "� un limite imposto dalla natura stessa, non si potr� mai superare". E’ molto importante capire questo punto, cio� che il rendimento della macchina di Carnot , ossia il teorema di Carnot, � puramente ideale, infatti � una costruzione puramente matematica, ma la sua importanza fisica � vitale. Abbiamo forse senza accorgersene resi un po’ pi� espliciti i due enunciati di Clausius e di Kelvin. Cecavamo infatti quello che � permesso fare, e adesso lo sappiamo :" Ci � permesso stare al di sotto del limite ". Sembra quasi una presa in giro, ma non lo �, il sapere dell’ esistenza di questo limite ci rende consapevoli di quello che non possiamo fare e quindi anche di quello che possiamo fare. Quindi se il limite � 1 ed � irraggiungibile, significa che nella nostra vita abbiamo solo a che fare con fenomeni che sfruttano l’energia in un modo non totalmente proficuo, cio� tutto quello che facciamo non ha un rendimento del 100%. Detto in altre parole, sempre in ogni istante una parte dell’ energia che utilizziamo va persa. Questo fatto conduce ad una ovvia domanda, poich� se ho tre caramelle e ne predo una mi chiedo:" Ma dove diavolo � andata a finire?". Bene, questa � la stessa domanda che si sono posti i fisici. La risposta che si sono dati �:

Questa � la definizione matematica della Funzione di stato Entropia, il suo significato � quello di misurare la quantit� di energia che va perduta nei processi irreversibili, in quanto come una ovvia conseguanza del teorema di Carnot, soltanto le macchine di Carnot hanno perdita di energia nulla, quindi variazione di entropia nulla. A questo punto risulta ovvio dire che in un processo irreversibile,ossia naturale, non solo un po’ di energia viene persa, e questa differenza si pu� calcolare tramita la formula dell’ entropia, ma anche che questa energia persa va ad aumentare l’ entropia stessa. E’ come se l’ entropia avesse una sua esistenza e si nutrisse di un po’ dell’ energia che usiamo noi. Ma non � finito qua infatti si pu� dimostrare che l’ entropia in un sistema chiuso aumenta sempre ,e questo fissa un oggettivo scorrere del tempo . Ci ritroviamo quindi tra le mani una formula esteticamente gradevole e di importanza, essendo sicuro di non esagerare, ontologicamente essenziale, una formula che ci informa del concetto che ha pi� affascinato l’ uomo nel suo cammino evolutivo e che regola la nostra vita:

IL TEMPO

	Go]
				[Back
				[Home